विषय सूची
इस लेख में गणितीयकरण क्या है, को समझने का प्रयास करेंगे
गणितीयकरण क्या है
(मायने एवं प्रक्रिया)
आदिकाल से ही गणित का महत्व रहा है, जो शाश्वत सत्य है। विज्ञान एवं तकनीकी में विकास गणित से ही संभव हुआ है। और तो और हम रोजाना ही गणित से दो-चार होते रहते हैं। गणित सभी क्षेत्रों में विद्यमान है। शायद इसकी अमूर्तता के कारण इसे एक कठिन विषय मानते है। विद्यालयों में बच्चों को गणित विषय कठिन लगता है। इसे सबसे कठिन विषय के रूप में प्रचारित किया जाता रहा है। अतः गणितीयकरण क्या है पर विचार करना होगा । जबकि जिन बच्चों के लिए शिक्षक इसे आसान विषय कहते हैं वे भी बच्चों को कुछ संक्रियाएँ सिखा देने को पर्याप्त मान लेते हैं। दरअसल जब कोई शिक्षक किसी बच्चे के बारे में यह राय रखते हैं कि यह बच्चा गणित में होशयार है तो उनका आशय यही रहता है कि ये बच्चा जोड़ना-घटाना-गुणा-भाग आसानी से कर लेता है अर्थात बच्चा गणना करना सीख गया है। कहने का आशय है कि गणित सिखाते समय या व्यवहार में इसके उद्देश्यों की ओर ध्यान नहीं जाता। जबकि इसके विस्तृत और विशिष्ट उद्देश्य हमारे पाठ्यचर्या में उल्लेखित है। यदि ऐसा है तो सभी शिक्षकों को गणित सिखाने के पहले एक सवाल स्वयं से करना चाहिए कि गणित हम बच्चों को सिखाते ही क्यों है या इस विषय को क्यों सीखा जाए? गणित जैसे अमूर्त विषय के माध्यम से सीखे जाने वाले कौशल हमारे दैनिक जीवन में किस प्रकार सहायक होते हैं?
गणितीयकरण के मायने
इस लेख में हम कोशिश करेंगे कि गणित में गणितीयकरण के मायने स्पष्ट हो। सबसे पहले हम देखते हैं कि गणितीय क्रिया का शाब्दिक अर्थ क्या है? तो सीधा जवाब मिलता है कि गणितीयकरण तार्किक ढंग से सोचने, अमूर्तनों का निर्माण करने, तथा संचालित करने की योग्यता का विकास करना है। इससे हम गणितीय सूत्रों तक तक पहुँचते हैं। NCF 2005 में देखते हैं गणित के बारे में क्या कहता है-

जबकि गणित में सवाल हल करने के लिए बच्चों को गणितीय सूत्रों की रचना करने के बजाय गणितीय सूत्रों को याद करने पर ज़ोर दिया जाता है। सामान्य रूप से गणितीयकरण का संबंध गणित में विकसित अवधारणा, प्रक्रिया एवं विधि का ज्ञान के विभिन्न क्षेत्रों के उपयोग से है। इसके लिए हमें गणित शिक्षण के उद्देश्यों को केंद्र में रखना होगा। डेविड व्हीलर कहते हैं “ज्यादा गणित जानने की अपेक्षा कैसे गणितीयकरण किया जाय यह अधिक उपयोगी है।“ राष्ट्रीय पाठ्यचर्या की रूपरेखा – 2005 में कहा गया है – “गणितीयकरण के लिए छात्रों की योग्यता को विकसित करना ही गणित शिक्षा का मुख्य उद्देश्य है।“ तो फिर से सवाल उठता है कि आखिर ये गणितीयकरण है क्या? जैसा कि पहले कहा गया है कि गणितीय क्रिया का मतलब गणितीय सूत्रों तक पहुँचना है। जब कोई व्यक्ति / बच्चा अपने सभी क्रियाकलापों तथा व्यवहार में व्यवस्थित एवं क्रमबद्ध रूप से अपने आपको गणितीय सटीकता के साथ प्रदर्शित करने की क्षमता प्राप्त कर लेता है। तब हम कह सकते हैं कि बच्चे ने गणितीयकरण की कौशल हासिल कर ली है।

अब आगे सवाल उठता है कि गणितीयकरण या गणितीय सूत्रों तक पहुँचना बच्चों को कैसे सिखाया जाय?
गणितीयकरण की क्षमताएँ
गणितीयकरण की प्रक्रिया को समझने से पहले हम ये जान लेते हैं कि इस गणितीयकरण में कौन-कौन सी क्षमताएँ शामिल है जिस पर काम करने से बच्चों में गणितीयकरण के कौशल विकसित होने की संभावना बढ़ जाएगी। ये क्षमताएँ हैं- समस्या समाधान, परीक्षणों के माध्यम से समस्याओं का हल ढूँढना, तर्क एवं प्रमाण, गणितीय सोच आदि । और इन सबका कुशलता पूर्वक उपयोग करते हुए गणितीय सूत्र की रचना करना सबसे महत्वपूर्ण है। तो क्या हमारे बच्चे गणितीय सूत्रों की रचना करने में समर्थ हो रहे है? इसके लिए जरूरी है कि बच्चों को रटना सिखाने के बजाय समस्या को समझने की क्षमता विकसित करके उसका हल ढूंढ कर गणित का उपयोग करना सीखें।
आइये अब थोड़ा इस बात पर विचार करते हैं कि गणितीयकरण के कौशल विकसित करने की प्रक्रिया क्या हो सकती है? इसके लिए सबसे पहले एक समस्या लेते हैं और देखते हैं कि किस प्रक्रिया से बच्चे गणितीयकरण या किसी समस्या के हल के लिए सूत्रों की रचना करने में सक्षम हो पाते हैं।
हाँ तो समस्या है- कक्षा का क्षेत्रफल निकालना। यहाँ यह ध्यान रखना होगा कि बच्चों में क्षेत्रफल की अवधारणा भी स्पष्ट हो जाए और यह भी समझ जाएँ कि क्षेत्रफल निकालने का सूत्र कैसे बना? या बन गया? सबसे पहले आमतौर पर प्रचलित प्रक्रिया पर दृष्टिपात करते है।
इसके लिए सबसे पहले हम बच्चों को इसका सूत्र बता देते हैं – लंबाई x चौड़ाई = क्षेत्रफल । अब किसी स्थान की लंबाई और चौड़ाई नाप कर इसे सूत्र में पिरो कर क्षेत्रफल ज्ञात करना सीखा देते हैं। दरअसल इस प्रक्रिया में हम बच्चों को सिखा नहीं रहे होते हैं बल्कि रटा रहे होते हैं। इससे बच्चों में क्षेत्रफल की अवधारणा भी नहीं बनती केवल क्षेत्रफल का सूत्र उनके मस्तिष्क में छप जाती है और इसे ही हम बच्चों का सीखना मान लेते हैं।
अब क्षेत्रफल ज्ञात करने और सूत्र तक पहुँचने की एक और प्रक्रिया को देखते हैं। इस प्रक्रिया में हमारा उद्देश्य होगा-
- · बच्चों में क्षेत्रफल की अवधारणा स्पष्ट करना ।
- · क्षेत्रफल के लिए सूत्र तक पहुंचना या सूत्र बनाना तथा
- · संवैधानिक मूल्यों को कक्षा प्रक्रिया में स्थान देना।
प्रक्रिया – 1 क्षेत्रफल की अवधारणा की समझ-
o 5-5 बच्चों का (सुविधानुसार इससे ज्यादा भी) छोटे-छोटे समूह बनाएँ। प्रत्येक समूह को गोल घेरे में बैठाएँ।
o प्रत्येक समूह को 3 x 3 फीट का चार्ट पेपर उपलब्ध कराएं। (ये साइज़ अन्य भी हो सकता है)। साथ ही 1 x 1 फीट एक एक छोटा चार्ट पेपर का टुकड़ा अलग से दें।
o अब निर्देश दें या सभी से कहें या सभी से पुछें कि इस छोटे चार्ट पेपर के टुकड़े को बड़े चार्ट पेपर में कितनी बार रखें कि यह बड़े चार्ट पेपर को पूरा माप कर लेगा? जितनी बार रखा जा सकता है उसकी संख्या लिखें ।
o जो संख्या मिलेगी उसी संख्या के बराबर बड़े चार्ट पेपर का माप होगा जिसे गणित की भाषा में क्षेत्रफल कहेंगे। यहाँ बच्चों से विस्तार से चर्चा करें और कहें कि किसी माप के द्वारा किसी स्थान को जितनी बार ढँक लेता है वही माप उस स्थान का क्षेत्रफल कहलाता है।
o अब इसे लिखने का तरीका भी बता दें कि बड़े चार्ट पेपर का क्षेत्रफल 9 वर्ग फीट होगा।
उपरोक्त प्रक्रिया की तरह कक्षा में उपलब्ध टेबल का क्षेत्रफल – ब्लेकबोर्ड का क्षेत्रफल निकालने का अभ्यास कराएं। अब तक की प्रक्रिया में बच्चे ये जान लेंगे कि कि क्षेत्रफल क्या होता है और इसे कैसे लिखा जाता है।
अब बारी आती है उस प्रक्रिया कि जिसमे बच्चे क्षेत्रफल निकालने के सूत्र तक स्वयं पहुंचे या सूत्र की रचना करें अर्थात गणितीयकरण कर पाएँ।
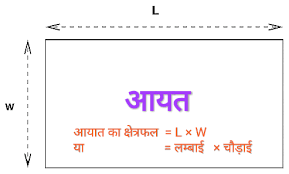
प्रक्रिया – 2 क्षेत्रफल के लिए सूत्र की रचना करना –
o अब बच्चों के सामने यह सवाल रखें कि यदि इस कक्षा / कमरे का क्षेत्रफल ज्ञात करना हो तो हमें क्या करना होगा? यहाँ बच्चों को सोचने का पर्याप्त समय दें, उनके बताए तरीकों को ध्यान से सुनें और उन तरीकों में आने वाली कठिनाइयों पर चर्चा करें । जैसे बच्चे कहें कि कमरे में छोटे चार्ट के टुकड़े को रख-रख कर गिन लेंगे। तो उनका ध्यान दिलाएँ कि इसमे तो बहुत समय लग जाएगा। तो फिर क्या करें कि आसानी से कमरे का क्षेत्रफल निकल जाए?
o यहाँ बच्चों से कहें कि पहले उपयोग में लाए बड़े चार्ट पेपर की लंबाई और चौड़ाई एक बार ज्ञात कर लिख लें और दोनों संख्या को आपस में गुणा कर मिलने वाली संख्या का मिलान का पता करें कि पूर्व प्रक्रिया से प्राप्त संख्या ही है या अलग है। (जाहीर है बच्चे कहेंगे कि वही संख्या (9) है)।
o बच्चों को फिर सोचने का मौका दें और उन्हें इस निष्कर्ष पर पहुँचने में उनकी मदद करें कि किसी स्थान का क्षेत्रफल निकालने के लिए उस स्थान की लंबाई और चौड़ाई का गुणन करने से भी हमें क्षेत्रफल प्राप्त हो जाता है। अतः क्षेत्रफल निकालने का सूत्र हुआ- लंबाई x चौड़ाई = क्षेत्रफल ।
उपरोक्त दोनों प्रक्रियाओं में आपने गौर किया कि बच्चे अपनी सक्रियता से क्षेत्रफल की समझ बना रहे थे। दोनों ही प्रक्रिया में शिक्षक की भूमिका एक सुविधादाता के रूप में मान्य रही। इस प्रकार बच्चे क्षेत्रफल की अवधारणात्मक समझ के साथ सूत्र तक पहुँच रहे थे। जिसे हम ‘गणितीयकरण के कौशल पर काम करना’ कह सकते हैं।
‘संवैधानिक मूल्यों को कक्षा प्रक्रिया में स्थान देना’ को भी हमने ऊपर उद्देश्य में लिखा है। तो आपका सवाल होगा कि यह उद्देश्य कैसे पूरा हुआ? गौर करें हमने बच्चों को छोटे – छोटे समूह में कार्य करने का अवसर दिया, इससे बच्चों में मिलजुल कर सहयोग की भावना जैसे मूल्य विकसित होंगे। इसी तरह कक्षा की प्रक्रिया में चर्चा को मुख्य स्थान दिया। जो प्रजातन्त्र की मुख्य विशेषता है।
साथियो, अब आप एक अन्य समस्या लें और बच्चों को गणितीयकरण तक ले जाने की कक्षा प्रक्रिया पर विचार करें। जैसे कि यदि एक हजार लीटर की धारिता वाले पानी की टंकी का निर्माण करना हो तो धारिता की अवधारणात्मक समझ एवं सूत्र रचना की प्रक्रिया क्या होगी?
आशा है आपको गणितीयकरण क्या है लेख अच्छा लगा होगा।


