
Teachers’ Problem-Solving Key: गणित सीखने का नया नजरिया
Teachers’ Problem-Solving Key वास्तव में गणित सिखाने और सीखने का एक नया नजरिया प्रस्तुत करता है। हाल ही में अपनी संस्था में आयोजित एक क्षमतावर्धन कार्यशाला में मुझे इस दृष्टिकोण को व्यवहार में देखने और समझने का अवसर मिला। दिलचस्प बात यह है कि प्रारम्भिक शिक्षा के बाद मैं कभी गणित का नियमित विद्यार्थी नहीं रहा, लेकिन शायद यही कारण था कि गणित को लेकर मेरे भीतर एक अलग तरह की जिज्ञासा हमेशा बनी रही। कार्यशाला के दौरान जब भी कोई नई अवधारणा सामने आती, मुझे बार-बार वे पल याद आते जब बच्चों के साथ काम करते हुए गणित की समस्याओं को हल करने की कोशिश करता था — ठीक वैसे ही जैसे Teachers’ Problem-Solving Key में सुझाया गया है — कि शिक्षक स्वयं समस्या-समाधान की प्रक्रिया में शामिल होकर बच्चों के सीखने को बेहतर दिशा दे सकते हैं।
बुनियादी साक्षरता एवं इबारती सवाल
बुनियादी साक्षरता एवं इबारती सवाल (Foundational Literacy and Word Problems) हम सब जानते हैं कि प्राथमिक कक्षाओं में गणित के प्रति बच्चों की जिज्ञासा बहुत स्वाभाविक होती है। फिर भी, अक्सर यह देखा गया है कि जब बच्चे इबारती सवाल (Word Problems) का सामना करते हैं, तो वे उलझ जाते हैं। आमतौर पर हमारी राय होती है कि यदि बच्चा सवाल हल नहीं कर पा रहा है, तो इसका कारण यही है कि वह पढ़ नहीं सकता। इसे हम सीधे तौर पर FL अर्थात Foundational Literacy की समस्या मान लेते हैं। इस सोच के साथ हम बिना गहराई में गए ही अगले कदम बढ़ा लेते हैं।
लेकिन अनुभव कुछ और भी कहता है। कई बार ऐसे बच्चे, जिन्हें पढ़ना भली-भाँति आता है, वे भी सवाल पढ़ते ही शिक्षक से पूछ बैठते हैं – “सर, इसमें जोड़ना है या घटाना?” यह स्थिति इस ओर संकेत करती है कि समस्या केवल पढ़ने–लिखने की नहीं है, बल्कि समस्या को समझने और समाधान की दिशा तय करने की क्षमता से जुड़ी हुई है, जिसे इस Teachers’ Problem-Solving Key के माध्यम से हम समझने का प्रयास करेंगे।

यही वह बिंदु है जहाँ गणितज्ञ जॉर्ज पोल्या का दृष्टिकोण अत्यंत उपयोगी सिद्ध होता है। पोल्या ने समस्या समाधान के लिए चार सरल किन्तु महत्वपूर्ण चरण बताए हैं, ये चरण केवल गणित ही नहीं, जीवन की किसी भी समस्या के समाधान में सहायक हो सकते हैं।
गणितज्ञ जॉर्ज पोल्या का दृष्टिकोण हमें यह समझने में मदद करता है कि गणित शिक्षा केवल संख्याओं और सूत्रों तक सीमित नहीं है, बल्कि यह बच्चों में सोचने, तर्क करने और समस्याओं को हल करने की क्षमता विकसित करने का माध्यम है। जब बच्चे किसी समस्या का समाधान ढूँढने का प्रयास करते हैं, तो वे केवल उत्तर ही नहीं खोजते, बल्कि सोचने की एक पद्धति भी सीखते हैं। इसी संदर्भ में प्रसिद्ध गणितज्ञ जॉर्ज पोल्या (George Polya) ने समस्या समाधान की चार सीढ़ियाँ (Four Steps of Problem Solving) बताई हैं। यह पद्धति न केवल गणित के लिए उपयोगी है, बल्कि जीवन की अन्य समस्याओं को हल करने में भी सहायक है।
यदि हम चाहते हैं कि गणित विषय पर कार्य करते हुए प्राथमिक स्तर के बच्चों के लिए सीखना और भी आसान हो, तो जॉर्ज पोल्या के बताए चार चरणों के साथ हम दो अतिरिक्त चरण (सुझावात्मक) भी जोड़ सकते हैं। चित्र में कुल 6 चरणों को उद्देश्य के साथ नीचे दिया गया है-
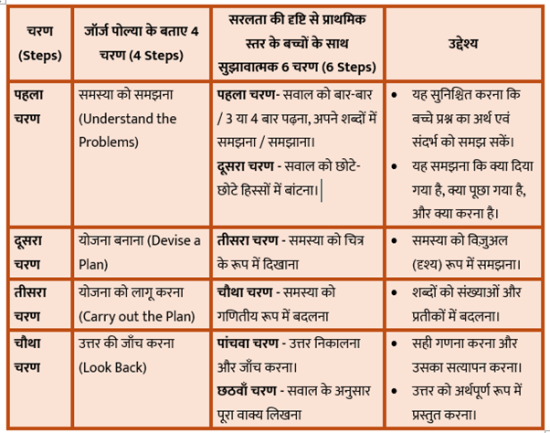
अब एक उदाहरण SCERT छत्तीसगढ़ द्वारा प्रकाशित कक्षा 4 की गणित पुस्तक से एक उदाहरण लेकर, जॉर्ज पोल्या के चार चरणों के साथ इन दो नए चरणों को मिलाकर हल करने का प्रयास करें।
उदाहरण: पहला पेड़, तीसरे पेड़ से 45 मीटर 50 सेंटीमीटर की दूरी पर है। दूसरा पेड़, तीसरे पेड़ से 25 मीटर 20 सेंटीमीटर की दूरी पर है। बताओ पहले व दूसरे पेड़ के बीच में कितनी दूरी है?
चरण-1: प्रश्न/सवाल/समस्या को बच्चों के समक्ष बार-बार पढ़ना या अलग-अलग बच्चों को बार-बार पढ़ने का अवसर देना। जिसका उद्देश्य है- यह सुनिश्चित करना कि प्रश्न का अर्थ एवं संदर्भ को बच्चे समझ सकें।
चरण-2: सवाल को छोटे-छोटे हिस्सों में बांटना। जिसका उद्देश्य है-
- यह समझना कि क्या दिया गया है (पहला पेड़ से तीसरे पेड़ की दूरी एवं दूसरा पेड़ का तीसरे पेड़ की दूरी);
- क्या पूछा गया है (पहले व दूसरे पेड़ के बीच की दूरी) और
- क्या करना है (जोड़ना है या घटाना है)।
उपरोक्त हिस्सों को underline करते जाना। कुछ इस तरह-
पहला पेड़, तीसरे पेड़ से 45 मीटर 50 सेंटीमीटर की दूरी पर है। दूसरा पेड़, तीसरे पेड़ से 25 मीटर 20 सेंटीमीटर की दूरी पर है। बताओ पहले व दूसरे पेड़ के बीच में कितनी दूरी है?
तीसरा चरण – समस्या को चित्र के रूप में दिखाना जिसका उद्देश्य है- समस्या को विज़ुअल (दृश्य) रूप में समझना।
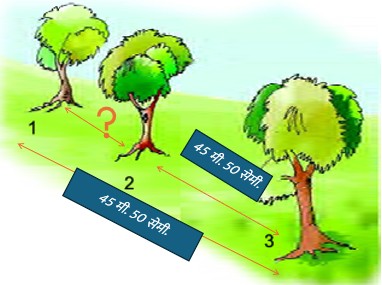
चौथा चरण – समस्या को गणितीय रूप में बदलना जिसका उद्देश्य है- शब्दों को संख्याओं और प्रतीकों में बदलना।कुछ इस तरह –

पांचवा चरण – उत्तर निकालना और जाँच करना। जिसका उद्देश्य है सही गणना करना और उसका सत्यापन करना। एवं उत्तर की जांच करना-
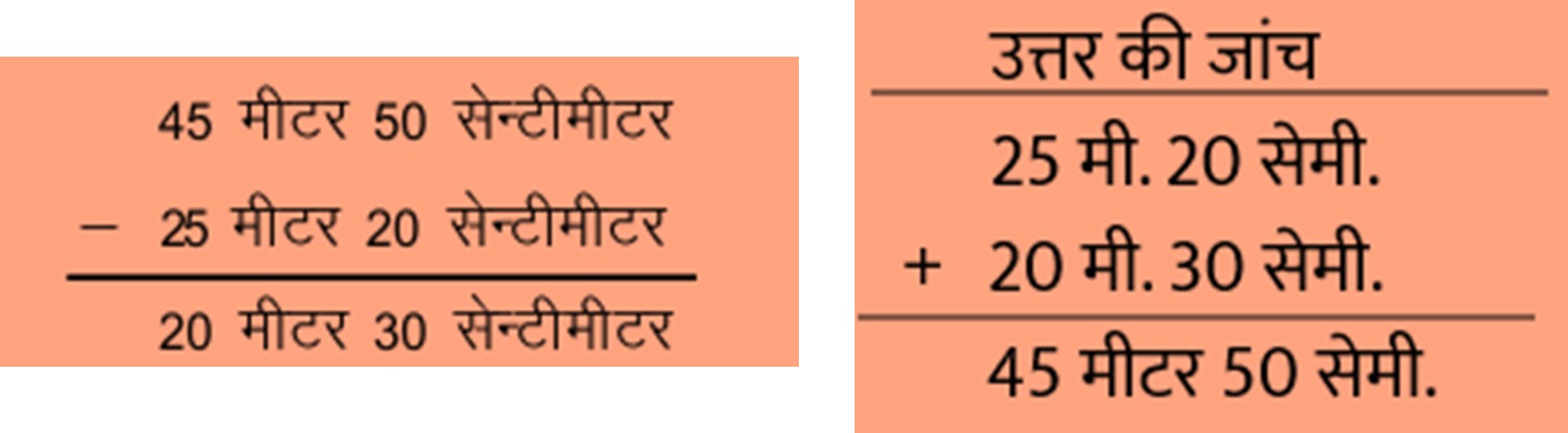
छठवाँ चरण – सवाल के अनुसार पूरा वाक्य लिखना अर्थात उत्तर को अर्थपूर्ण रूप में प्रस्तुत करना-
अतः: पहले एवं दूसरे पेड़ की दूरी 20 मीटर 30 सेंटीमीटर है।
इस प्रक्रिया से मिली सीख को बच्चों के सामने दोबारा रखें। इस तरह-
इस उदाहरण से हमने सीखा कि—
- पहले सवाल को ध्यान से पढ़ना चाहिए।
- फिर यह सोचना चाहिए कि कौन सा तरीका अपनाएँ।
- उसके बाद हल करना चाहिए।
- और अंत में उत्तर की जाँच करनी चाहिए।
यही Georg Polya की चार सीढ़ियाँ हैं जो हमें समस्या हल करने का सही तरीका सिखाती हैं, का लेख पढ़ने के लिए –
https://www.academy.vic.gov.au/resources/polyas-problem-solving-process
निष्कर्ष
पोल्या की यह चार-चरणीय पद्धति (समस्या को समझना, योजना बनाना, योजना को लागू करना और उत्तर की जाँच करना) विद्यार्थियों को केवल गणितीय समस्याएँ हल करना नहीं सिखाती, बल्कि जीवन में आने वाली कठिनाइयों से जूझने का व्यावहारिक तरीका भी सिखाती है। यदि हम प्राथमिक स्तर से ही बच्चों को इस ढंग से सोचने की आदत डालें, तो वे आगे चलकर आत्मनिर्भर, तार्किक और आत्मविश्वासी समस्या समाधानकर्ता बन सकते हैं।
इस तरह बच्चों को Polya’s Four चरण के ज़रिए समस्या-समाधान की आदत पड़ती है और वे व्यवस्थित तरीके से सोचने लगते हैं। यही गणित शिक्षण का उद्देश्य भी है।
अन्य महत्वपूर्ण लेख-


